Recursion

1. What Is Recursion?

2. The Three Laws of Recursion

3. Tower of Hanoi

4. Exploring the maze

5. Dynamic Programming

4.2 What Is Recursion?

Recursion is a method of solving problems that involves breaking a problem down into smaller and smaller subproblems until you get to a small enough problem that it can be solved trivially.

Usually recursion involves a function calling itself. It allows us to write elegant solutions to problems that may otherwise be very difficult to program!

4.3 Calculating the Sum of a List of Numbers

Suppose that you want to calculate the sum of a list of numbers such as: [1,3,5,7,9]. An iterative function that computes the sum is shownbelow:

def list_sum(num_list):
    the_sum = 0
    for i in num_list:
        the_sum = the_sum + i
    return the_sum

print(list_sum([1, 3, 5, 7, 9]))

25

The function uses an accumulator variable (the_sum) to compute a running total of all the numbers in the list by starting with 0.

If we do not have loops. How would you compute the sum of a list of numbers?

You might start by recalling that addition is a function that is defined for two parameters, a pair of numbers. To redefine the problem from adding a list to adding pairs of numbers, we could rewrite the list as a fully parenthesized expression. Such an expression looks like this:

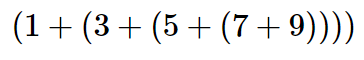
Notice that the innermost set of parentheses, $(7+9)$, is a problem that we can solve without a loop or any special constructs! In fact, we can use the following sequence of simplifications to compute a final sum:

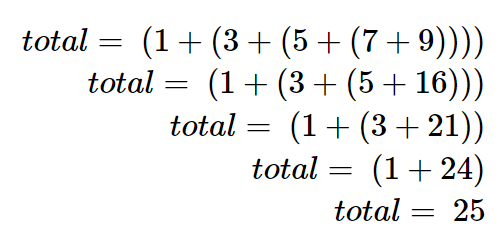
First, let’s restate the sum problem in terms of Python lists. We might say the sum of the list num_list is the sum of the first element of the list (num_list[0]) and the sum of the numbers in the rest of the list (num_list[1:]). To state it in a functional form:

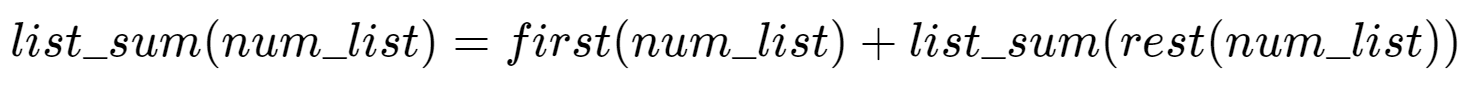
def list_sum(num_list):
    if len(num_list) == 1:
        return num_list[0]
    else:
        return num_list[0] + list_sum(num_list[1:])

print(list_sum([1, 3, 5, 7, 9]))

25

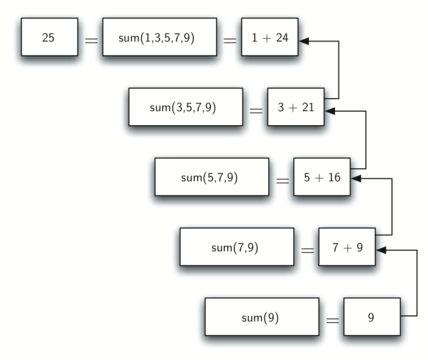
Figure below shows the series of recursive calls that are needed to sum the list. You should think of this series of calls as a series of simplifications.

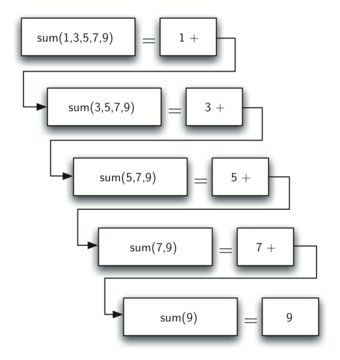
When we reach the point where the problem is as simple as it can get, we begin to piece together the solutions of each of the small problems until the initial problem is solved!

4.4 The Three Laws of Recursion

Like robots in Asimov’s stories, all recursive algorithms must obey three important laws:

1. A recursive algorithm must have a base case.

2. A recursive algorithm must change its state and move toward the base case.

3. A recursive algorithm must call itself recursively.

First, a base case is the condition that allows the algorithm to stop recursing. A base case is typically a problem that is small enough to solve directly. In the list_sum() algorithm the base case is a list of length 1.

A change of state means that some data that the algorithm is using is modified. Usually the data that represents our problem gets smaller in some way. In the list_sum() algorithm our primary data structure is a list. Since the base case is a list of length 1, a natural progression toward the base case is to shorten the list.

The final law is that the algorithm must call itself. This is the very definition of recursion.

As a novice programmer, you have learned that functions are good because you can take a large problem and break it up into smaller problems. The smaller problems can be solved by writing a function to solve each problem.

When we talk about recursion it may seem that we are talking ourselves in circles. We have a problem to solve with a function, but that function solves the problem by calling itself! We are solving a problem by breaking it down into a smaller and easier problems.

4.5 Converting an Integer to a String in Any Base

Suppose you want to convert an integer to a string in some base between binary and hexadecimal. For example, convert the integer 10 to its string representation in decimal as "10", or to its string representation in binary as "1010".

While there are many algorithms to solve this problem, including the algorithm discussed in the stack section, the recursive formulation of the problem is very elegant.

Let’s look at a concrete example using base 10 and the number 769. Suppose we have a sequence of characters corresponding to the first 10 digits, like convert_string = "0123456789". It is easy to convert a number less than 10 to its string equivalent by looking it up in the sequence.

If we can arrange to break up the number 769 into three single-digit numbers, 7, 6, and 9, then converting it to a string is simple. A number less than 10 sounds like a good base case.

Knowing what our base is suggests that the overall algorithm will involve three components:

1. Reduce the original number to a series of single-digit numbers.

2. Convert the single digit-number to a string using a lookup.

3. Concatenate the single-digit strings together to form the final result.

The next step is to figure out how to change state and make progress toward the base case.

Let’s consider what mathematical operations might reduce a number. The most likely candidates are division and subtraction. While subtraction might work, it is unclear what we should subtract from what. Integer division with remainders gives us a clear direction!

Using integer division to divide 769 by 10, we get 76 with a remainder of 9. This gives us two good results.

1. The remainder is a number less than our base that can be converted to a string immediately by lookup.

2. We get a number that is smaller than our original and moves us toward the base case of having a single number less than our base.

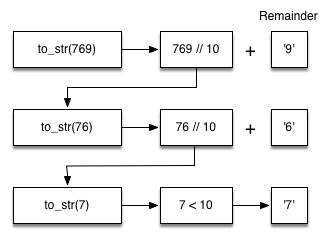
Now our job is to convert 76 to its string representation. Again we will use integer division plus remainder to get results of 7 and 6 respectively.

# The algorithm outlined above for any base between 2 and 16.
def to_str(n, base):
    convert_string = "0123456789ABCDEF"
    if n < base:
        return convert_string[n]
    else:
        return to_str(n // base, base) + convert_string[n % base]

print(to_str(1453, 16))

5AD

Notice that in line 3 we check for the base case where n is less than the base we are converting to. When we detect the base case, we stop recursing and simply return the string from the convert_string sequence.

In line 6 we satisfy both the second and third laws–by making the recursive call and by reducing the problem size–using division.

Let’s trace the algorithm; this time we will convert the number 10 to its base 2 string representation ("1010"):

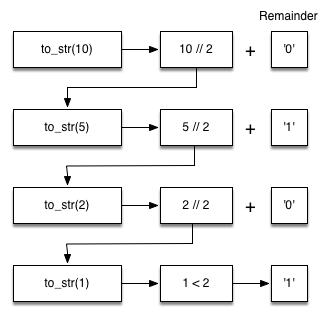
It looks like the digits are in the wrong order. The algorithm works correctly because we make the recursive call first on line 6, then we add the string representation of the remainder.

If we reversed returning the convert_string lookup and returning the to_str() call, the resulting string would be backward! But by delaying the concatenation operation until after the recursive call has returned, we get the result in the proper order! This should remind you of our discussion of stacks back in the previous chapter.

Exercsie: Write a function using recursion that takes a string as a parameter and returns a new string that is the reverse of the old string.

def reverse(s):
    return s

assert reverse("hello") == "olleh"

4.6 Stack Frames: Implementing Recursion

Suppose that instead of concatenating the result of the recursive call to to_str() with the string from convert_string, we modified our algorithm to push the strings onto a stack instead of making the recursive call:

import sys
sys.path.append("./pythonds3/")

from pythonds3.basic import Stack

def to_str(n, base):
    r_stack = Stack()
    convert_string = "0123456789ABCDEF"
    while n > 0:
        if n < base:
            r_stack.push(convert_string[n])
        else:
            r_stack.push(convert_string[n % base])
        n = n // base
    res = ""
    while not r_stack.is_empty():
        res = res + str(r_stack.pop())
    return res

print(to_str(1453, 16))

5AD

Each time we make a call to to_str(), we push a character on the stack. Returning to the previous example we can see that after the fourth call to to_str() the stack would look like Figure below:

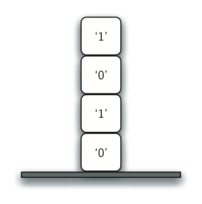
Notice that now we can simply pop the characters off the stack and concatenate them into the final result, "1010".

The previous example gives us some insight into how Python implements a recursive function call. When a function is called in Python, a stack frame is allocated to handle the local variables of the function.

When the function returns, the return value is left on top of the stack for the calling function to access.

Figure below illustrates the call stack after the return statement:

Notice that the call to to_str(2 // 2, 2) leaves a return value of "1" on the stack. This return value is then used in place of the function call (to_str(1, 2)) in the expression "1" + convert_string[2 % 2], which will leave the string "10" on the top of the stack.

In this way, the Python call stack takes the place of the stack we used explicitly. In our list summing example, you can think of the return value on the stack taking the place of an accumulator variable.

The stack frames also provide a scope for the variables used by the function. Even though we are calling the same function over and over, each call creates a new scope for the variables that are local to the function.

4.10 Tower of Hanoi

The Tower of Hanoi puzzle was invented by the French mathematician Edouard Lucas in 1883. He was inspired by a legend that tells of a Hindu temple where the puzzle was presented to young priests.

At the beginning of time, the priests were given three poles and a stack of 64 gold disks, each disk a little smaller than the one beneath it. Their assignment was to transfer all 64 disks from one of the three poles to another, with two important constraints.

1. They could only move one disk at a time.
2. They could never place a larger disk on top of a smaller one.

The priests worked very efficiently, day and night, moving one disk every second. When they finished their work, the legend said, the temple would crumble into dust and the world would vanish.

Although the legend is interesting, you need not worry about the world ending any time soon. The number of moves required to correctly move a tower of 64 disks is $2^{64}-1 = 18,446,744,073,709,551,615$. At a rate of one move per second, that is $584,942,417,355$ years!

Figure below shows an example of a configuration of disks in the middle of a move from the first peg to the third. Notice that, as the rules specify, the disks on each peg are stacked so that smaller disks are always on top of the larger disks:

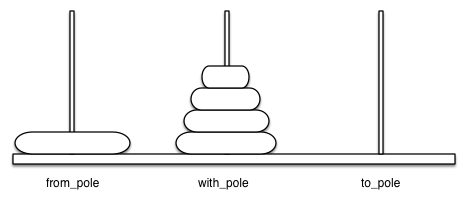
Let’s think about this problem from the bottom up. Suppose you have a tower of five disks, originally on peg one. If you already knew how to move a tower of four disks to peg two, you could then easily move the bottom disk to peg three, and then move the tower of four from peg two to peg three.

But what if you do not know how to move a tower of height four? Suppose that you knew how to move a tower of height three to peg three; then it would be easy to move the fourth disk to peg two and move the three from peg three on top of it.

But what if you still do not know how to do this? Surely you would agree that moving a single disk to peg three is easy enough, trivial you might even say. This sounds like a base case in the making.

Here is a high-level outline of how to move a tower of height $h$ from the starting pole to the goal pole, using an intermediate pole:

1. Move a tower of height $h-1$ from the starting pole to an intermediate pole via the goal pole.

2. Move the remaining disk from the starting pole to the final pole.

3. Move the tower of height $h-1$ from the intermediate pole to the goal pole via the starting pole.

The simplest Tower of Hanoi problem is a tower of one disk. In this case, we need move only a single disk to its final destination. A tower of one disk will be our base case. In addition, the steps outlined above move us toward the base case by reducing the height of the tower in steps 1 and 3.

def move_tower(height, from_pole, to_pole, with_pole):
    if height >= 1:
        move_tower(height - 1, from_pole, with_pole, to_pole)
        move_disk(from_pole, to_pole)
        move_tower(height - 1, with_pole, to_pole, from_pole)

def move_disk(from_p, to_p):
    print("moving disk from", from_p, "to", to_p)

move_tower(3, "A", "B", "C")

moving disk from A to B
moving disk from A to C
moving disk from B to C
moving disk from A to B
moving disk from C to A
moving disk from C to B
moving disk from A to B

The base case is the tower of height 0; in this case there is nothing to do, so the move_tower() function returns. The important thing to remember about handling the base case this way is that simply returning from move_tower() is what finally allows the move_disk function to be called.

Now that you have seen the code for both move_tower and move_disk, you may be wondering why we do not have a data structure that explicitly keeps track of what disks are on what poles.

Here is a hint: if you were going to explicitly keep track of the disks, you would probably use three Stack objects, one for each pole. The answer is that Python provides the stacks that we need implicitly through the call stack!

4.11 Exploring a Maze

In this section we will look at a problem that has relevance to the expanding world of robotics: how do you find your way out of a maze?

The problem we want to solve is to help our turtle find its way out of a virtual maze. The maze problem has roots as deep as the Greek myth about Theseus, who was sent into a maze to kill the Minotaur.

Theseus used a ball of thread to help him find his way back out again once he had finished off the beast. In our problem we will assume that our turtle is dropped down somewhere into the middle of the maze and must find its way out.

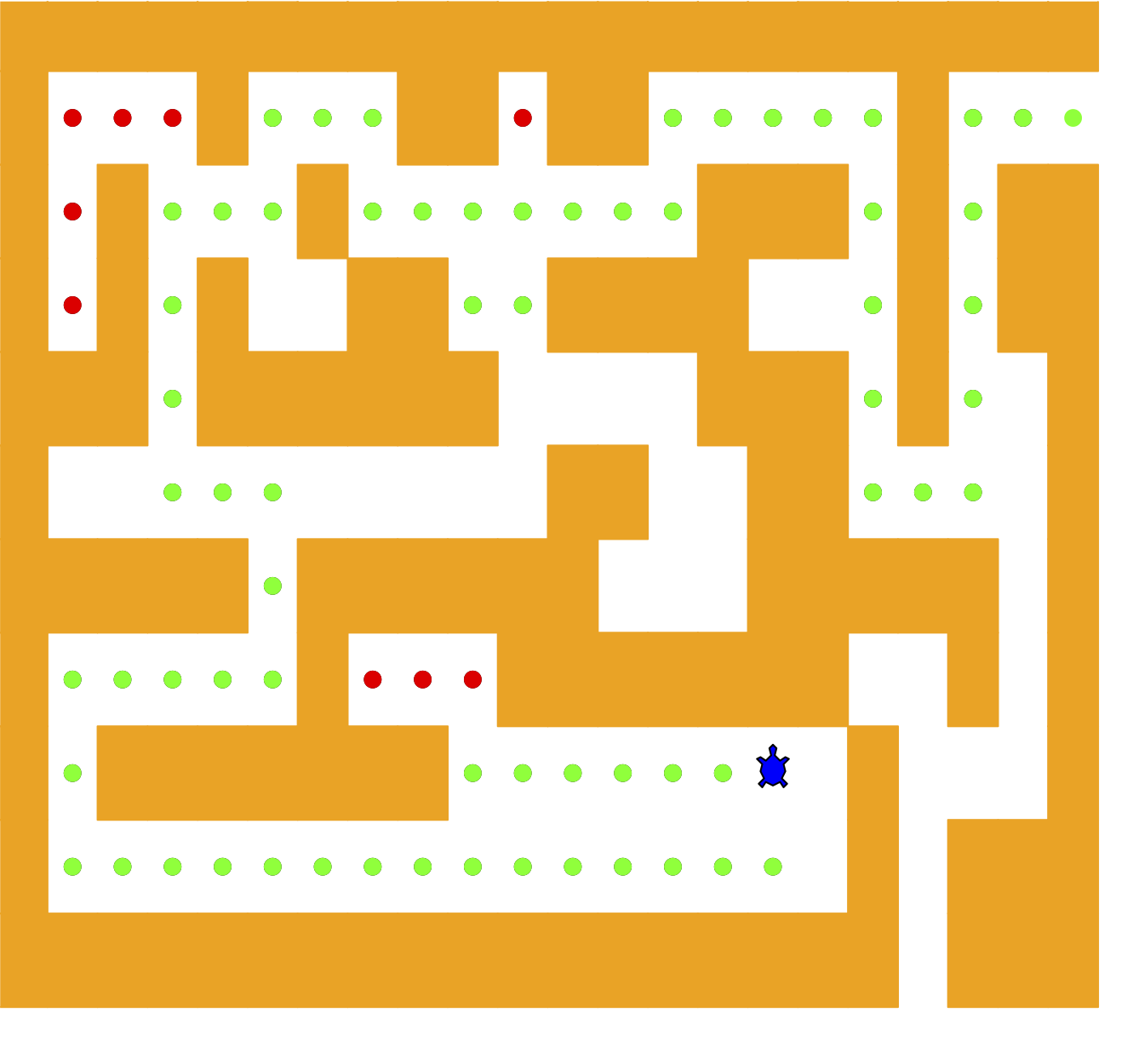
To make it easier for us we will assume that our maze is divided up into squares. Each square of the maze is either open or occupied by a section of wall. The turtle can only pass through the open squares of the maze. If the turtle bumps into a wall, it must try a different direction. Here is the procedure:

1. From our starting position we will first try going north one square and then recursively try our procedure from there.

2. If we are not successful by trying a northern path as the first step then we will take a step to the south and recursively repeat our procedure.

3. If south does not work then we will try a step to the West as our first step and recursively apply our procedure.

4. If north, south, and west have not been successful then we will apply the procedure recursively from a position one step to our east.

5. If none of these directions works then there is no way to get out of the maze and we fail.

Now that sounds easy, but there are a couple of details to talk about! Suppose we take our first recursive step by going north. By following our procedure, our next step would also be to the north. But if the north is blocked by a wall, we must look at the next step of the procedure and try going to the south.

Unfortunately, that step to the south brings us right back to our original starting place. If we apply the recursive procedure from there, we will just go back one step to the North and be in an infinite loop! So we must have a strategy to remember where we have been!

In this case we will assume that we have a bag of bread crumbs we can drop along our way. If we take a step in a certain direction and find that there is a bread crumb already on that square, we know that we should immediately back up and try the next direction in our procedure. As we will see when we look at the code for this algorithm, backing up is as simple as returning from a recursive function call.

As we do for all recursive algorithms, let us review the base cases. Some of them you may already have guessed based on the description in the previous paragraph. In this algorithm, there are four base cases to consider:

1. The turtle has run into a wall. Since the square is occupied by a wall, no further exploration can take place.

2. The turtle has found a square that has already been explored. We do not want to continue exploring from this position so we don’t get into a loop.

3. We have found an outside edge, not occupied by a wall. In other words, we have found an exit from the maze.

4. We have explored a square unsuccessfully in all four directions.

Now we will considering the following maze:

++++++++++++++++++++++
+   +   ++ ++     +
+ +   +       +++ + ++
+ + +  ++  ++++   + ++
+++ ++++++    +++ +  +
+          ++  ++    +
+++++ ++++++   +++++ +
+     +   +++++++  + +
+ +++++++      S +   +
+                + +++
++++++++++++++++++ +++

The Maze object will provide the following methods for us to use in writing our search algorithm:

1. __init__ Reads in a data file representing a maze, initializes the internal representation of the maze, and finds the starting position for the turtle.

2. draw_maze() Draws the maze in a window on the screen.

3. update_position() Updates the internal representation of the maze and changes the position of the turtle in the window.

4. is_exit() Checks to see if the current position is an exit from the maze.

The Maze class also overloads the index operator [] so that our algorithm can easily access the status of any particular square.

%%writefile maze.py

import turtle

START = "S"
OBSTACLE = "+"
TRIED = "."
DEAD_END = "-"
PART_OF_PATH = "O"

Overwriting maze.py

The __init__ method takes the name of a file as its only parameter. This file is a text file that represents a maze by using "+" characters for walls, spaces for open squares, and the letter "S" to indicate the starting position.

%%writefile -a maze.py
class Maze:
    def __init__(self, maze_filename):
        with open(maze_filename, "r") as maze_file:
            self.maze_list = [
                [ch for ch in line.rstrip("\n")]
                for line in maze_file.readlines()
            ]
        self.rows_in_maze = len(self.maze_list)
        self.columns_in_maze = len(self.maze_list[0])
        for row_idx, row in enumerate(self.maze_list):
            if START in row:
                self.start_row = row_idx
                self.start_col = row.index(START)
                break
        # This is for turtle module, do not worry about it
        self.x_translate = -self.columns_in_maze / 2
        self.y_translate = self.rows_in_maze / 2
        self.t = turtle.Turtle()
        self.t.shape("turtle")
        self.wn = turtle.Screen()
        self.wn.setworldcoordinates(
            -(self.columns_in_maze - 1) / 2 - 0.5,
            -(self.rows_in_maze - 1) / 2 - 0.5,
            (self.columns_in_maze - 1) / 2 + 0.5,
            (self.rows_in_maze - 1) / 2 + 0.5)
        self.current_speed = 6  # Default speed

Appending to maze.py

%%writefile -a maze.py
    # This is for turtle module, do not worry about it
    def draw_maze(self):
        self.t.speed(10)
        self.wn.tracer(0)
        for y in range(self.rows_in_maze):
            for x in range(self.columns_in_maze):
                if self.maze_list[y][x] == OBSTACLE:
                    self.draw_centered_box(
                        x + self.x_translate, -y + self.y_translate, "orange"
                    )
        self.t.color("black")
        self.t.fillcolor("blue")
        self.wn.update()
        self.wn.tracer(1)
    def draw_centered_box(self, x, y, color):
        self.t.up()
        self.t.goto(x - 0.5, y - 0.5)
        self.t.color(color)
        self.t.fillcolor(color)
        self.t.setheading(90)
        self.t.down()
        self.t.begin_fill()
        for i in range(4):
            self.t.forward(1)
            self.t.right(90)
        self.t.end_fill()

Appending to maze.py

%%writefile -a maze.py
    def update_position(self, row, col, val=None):
        if val:
            self.maze_list[row][col] = val
        self.move_turtle(col, row)
        if val == PART_OF_PATH:
            color = "green"
        elif val == OBSTACLE:
            color = "red"
        elif val == TRIED:
            color = "black"
        elif val == DEAD_END:
            color = "red"
        else:
            color = None
        if color:
            self.drop_bread_crumb(color)
    # This is for turtle module, do not worry about it
    def move_turtle(self, x, y):
        self.t.up()
        self.t.setheading(self.t.towards(x + self.x_translate, -y + self.y_translate))
        self.t.goto(x + self.x_translate, -y + self.y_translate)

    def drop_bread_crumb(self, color):
        self.t.dot(10, color)

Appending to maze.py

%%writefile -a maze.py
    def is_exit(self, row, col):
        return (
            row == 0
            or row == self.rows_in_maze - 1
            or col == 0
            or col == self.columns_in_maze - 1
        )

    def __getitem__(self, idx):
        return self.maze_list[idx]
    # This is for turtle module, do not worry about it
    def set_speed(self, speed):
        self.current_speed = speed
        self.t.speed(speed)

    def start_interactive_control(self):
        self.wn.listen()
        self.wn.onkey(lambda: self.set_speed(10), "f")
        self.wn.onkey(lambda: self.set_speed(3), "n")
        self.wn.onkey(lambda: self.set_speed(1), "s")

Appending to maze.py

%%writefile -a maze.py
def search_from(maze, row, column):
    # Try each of four directions from this point until we find a way out.
    maze.update_position(row, column)
    # Base Case return values:
    #  1. We have run into an obstacle, return false
    if maze[row][column] == OBSTACLE:
        return False
    #  2. We have found an already explored square
    if maze[row][column] in [TRIED, DEAD_END]:
        return False
    # 3. We have found an exit
    if maze.is_exit(row, column):
        maze.update_position(row, column, PART_OF_PATH)
        return True
    maze.update_position(row, column, TRIED)
    # Otherwise, use logical short circuiting to try each direction in turn (if needed)
    found = (
        search_from(maze, row - 1, column)
        or search_from(maze, row + 1, column)
        or search_from(maze, row, column - 1)
        or search_from(maze, row, column + 1))
    if found:
        maze.update_position(row, column, PART_OF_PATH)
    else:
        maze.update_position(row, column, DEAD_END)
    return found

Appending to maze.py

You will notice that in the recursive step there are four recursive calls to search_from(). It is hard to predict how many of these recursive calls will be used since they are all connected by or statements.

If the first call to search_from() returns True then none of the last three calls would be needed. You can interpret this as meaning that a step to (row - 1, column) (or north if you want to think geographically) is on the path leading out of the maze.

If there is not a good path leading out of the maze to the north then the next recursive call is tried, this one to the south. If south fails then try west, and finally east. If all four recursive calls return False then we have found a dead end.

%%writefile -a maze.py

my_maze = Maze("maze2.txt")
my_maze.draw_maze()
my_maze.update_position(my_maze.start_row, my_maze.start_col)

my_maze.start_interactive_control()
search_from(my_maze, my_maze.start_row, my_maze.start_col)

Appending to maze.py

%%writefile maze2.txt
++++++++++++++++++++++
+   +   ++ ++        +
      +     ++++++++++
+ +    ++  ++++ +++ ++
+ +   + + ++    +++  +
+          ++  ++  + +
+++++ + +      ++  + +
+++++ +++  + +  ++   +
+          + + S+ +  +
+++++ +  + + +     + +
++++++++++++++++++++++

Overwriting maze2.txt

!python maze.py

References

1. Textbook CH4